算法时间复杂度及P、NP、NP-Complete、NP-Hard问题
算法的时间复杂度
如果某个算法的复杂度可以表示为,即问题规模n出现在底数的位置,这种复杂度称为多项式时间复杂度;
如果某个算法的复杂度表示为或,这种复杂度称为指数型时间复杂度。
相同问题规模下(同时这个问题规模不是太小),指数型时间复杂度远远大于多项式时间复杂度。
当我们在解决一个问题时,我们选择的算法通常都需要是多项式时间复杂度的,指数型时间复杂度的算法是计算机所不能承受的(除非问题规模很小)。
P、NP、NP-Complete、NP-Hard问题
如果一个问题可以找到一个只有多项式复杂度的算法(这个算法可以在多项式时间内求得解),那这个问题就属于P(Polynomial)问题(即多项式问题);
无法找到任何多项式复杂度算法的可解问题,则称为指数型(Exponential)问题;
没有任何可解算法的问题,则称为不可解问题;
此外,我们关注多项式时间内是否可以验证一个解,如果可以,这个问题就被称为NP(Non-Deterministic Polynomial )问题(即非决定性多项式问题)。
由此可知,所有的P问题都是NP问题。
之所以要定义NP问题,是因为通常只有NP问题才可能找到多项式的算法。我们不会指望一个连多项式地验证一个解都不行的问题存在一个解决它的多项式级的算法。
在NP问题中,有这么一类问题,所有的NP问题在多项式时间内都可以归约成这类问题【注:“问题A可归约为问题B”有一个重要的直观意义:B的时间复杂度高于或者等于A的时间复杂度。】,这类问题被称为NPC(NP-Complete)问题【所以说,NPC问题的时间复杂度大于等于NP问题的时间复杂度,NP问题不比NPC问题难。 】。
如果能够证明任何一个NPC问题可以在多项式时间内求得解,就可以证明**P=NP?**这个困扰信息学的重要问题了。
而无论是不是NP问题,又有这么一类问题,所有的NP问题在多项式时间内都可以归约成这类问题,这类问题就被称为NPH(NP-Hard)问题;
NPC和NPH两者的区别是: 验证一个问题A是否为NP-Hard无须判断A是否属于NP,但是NPC问题必须首先是NP问题. 根据定义可知NPC ∈ NPH。
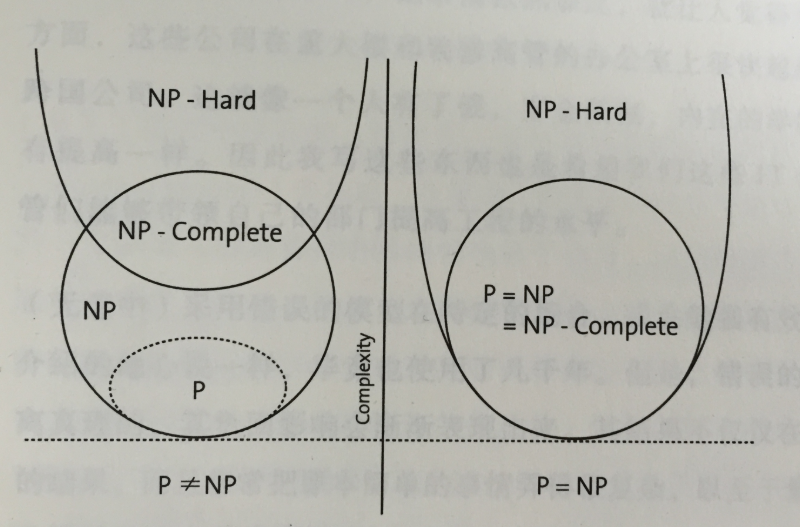
由于P=NP?并没有得到证明,因此,目前可以对问题作出这样的分类:
典型的NP-Hard问题
旅行商问题,即TSP问题(Traveling Salesman Problem),又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。 若有 20 个城,则排法就有种。在排列组合里 写起来轻松,但是一个大得不得了的数字。若每秒钟排一次,要排 年。旅行商问题可以归约到NPC问题。
参考文献
算法的时间复杂度和空间复杂度-总结
什么是P问题、NP问题和NPC问题
P/NP/NPC/NP-hard
NP-Hard问题浅谈
算法时间复杂度及P、NP、NP-Complete、NP-Hard问题
https://forskamse.github.io/2020/07/04/2020-07-04-Time_Complexity_of_Algorithms/